The Arrhenius Equation: A Closer Look
At the heart of understanding the temperature dependence of reaction rates lies the Arrhenius equation, a pivotal concept in chemical kinetics. This equation connects the rate constant of a chemical reaction with the temperature at which the reaction occurs, along with other fundamental constants.
[ k = Ae{-\frac{Ea}{RT}} ]
Rate Constant (( k )): This is a measure of the speed of a reaction. The rate constant is crucial because it directly influences how fast or slow a reaction proceeds. It varies with temperature, meaning that as the temperature changes, so does the speed of the reaction.
Arrhenius Constant (( A )): Often referred to as the pre-exponential factor, it is a constant that incorporates factors such as the frequency of molecules colliding with the correct orientation to react. It represents the maximum number of collisions resulting in a reaction per unit time under the most favorable conditions.
Activation Energy (( Ea )): This is the minimum energy required for a reaction to occur. It represents the energy barrier that reactants must overcome to transform into products. The concept of activation energy is central to understanding why certain reactions occur rapidly at higher temperatures.
Universal Gas Constant (( R )): A fundamental constant in chemistry and physics, ( R ) is the bridge between macroscopic and microscopic phenomena, linking temperature with individual molecular energy levels.
Temperature (( T )): Expressed in Kelvin, temperature is a measure of the thermal energy available to the reactant molecules. Higher temperatures provide more energy, increasing the proportion of molecules that can overcome the activation energy barrier.
Image courtesy of Julee Ashmead
Activation Energy and Its Role
The activation energy (( Ea )) is a critical factor in the Arrhenius equation. It defines the height of the energy barrier that reactants must overcome for a reaction to proceed. In essence, only a fraction of the total number of molecules possess enough kinetic energy to surpass this barrier at any given temperature. This fraction increases exponentially with temperature, as described by the Boltzmann distribution, leading to a higher reaction rate.
Temperature's Impact on Reaction Rates
The exponential relationship between the rate constant and temperature in the Arrhenius equation highlights the sensitivity of chemical reactions to temperature changes. Even small increases in temperature can lead to significant increases in the rate constant, and consequently, the reaction rate. This is because the distribution of molecular energies shifts to higher values with increasing temperature, enabling more molecules to have energies exceeding the activation energy.
Practical Implications
Understanding how temperature affects reaction rates is vital in industries where chemical reactions are controlled to synthesize products, such as pharmaceuticals and petrochemicals. It also plays a crucial role in food preservation, where lower temperatures are used to slow down the rate of spoilage reactions.
Calculations Involving the Arrhenius Equation
Using the Arrhenius equation in calculations allows chemists to predict the rate constant (( k )) at different temperatures, provided the activation energy (( Ea )) and the Arrhenius constant (( A )) are known. These calculations are pivotal in designing chemical processes and understanding reaction mechanisms.
Example Calculation
Let's consider a hypothetical reaction with an activation energy of ( 75 \, \text{kj mol}{-1} ) and an Arrhenius constant of ( 10{14} \, \text{s}{-1} ). To find the rate constant at 350 K, we apply the Arrhenius equation:
[ k = 10{14} e{-\frac{75000}{8.314 \times 350}} ]
Such calculations are instrumental in predicting how a reaction's rate will change with temperature, aiding in the optimization of industrial processes and laboratory experiments.
Experimental Determination and Graphical Analysis
The practical application of the Arrhenius equation extends to experimental work, where it is used to analyze reaction kinetics. By measuring the rate constant at various temperatures, chemists can plot data that yields valuable kinetic parameters.
Plotting ln(k) vs. 1/T
A linear plot of the natural logarithm of the rate constant (( \ln k )) against the reciprocal of the temperature (( \frac{1}{T} )) simplifies the analysis. This plot, known as the Arrhenius plot, should yield a straight line, from which the activation energy and the Arrhenius constant can be determined:
The slope of this line gives ( -\frac{Ea}{R} ), allowing the calculation of the activation energy.
The y-intercept provides the natural logarithm of the Arrhenius constant (( \ln A )), from which ( A ) can be directly obtained.
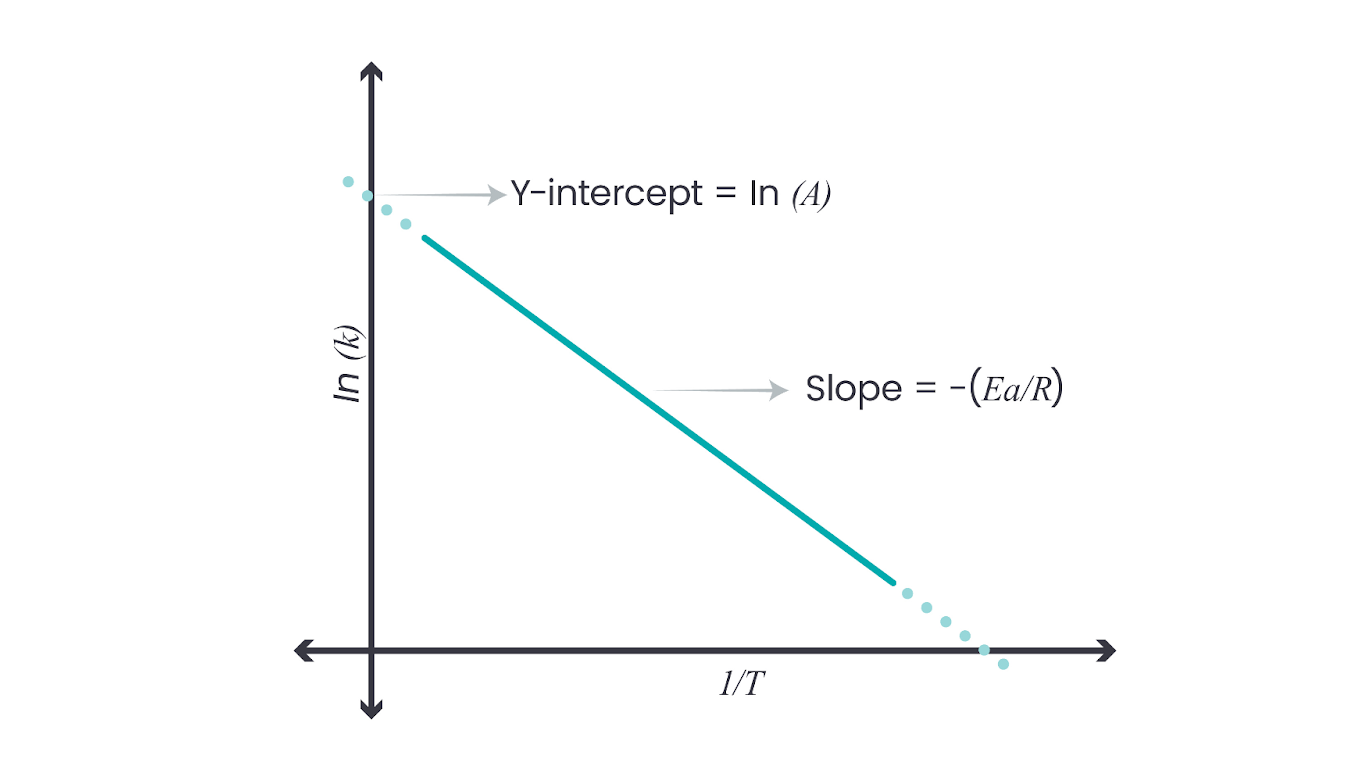
Image courtesy of Julee Ashmead
Case Study: Iodine Clock Reaction
Consider the iodine clock reaction, a classic experiment in chemical kinetics. By conducting this reaction at different temperatures and measuring the rate constant for each, students can plot ( \ln k ) against ( \frac{1}{T} ) to derive both ( Ea ) and ( A ). This hands-on approach not only reinforces theoretical concepts but also hones practical laboratory skills.
Skills and Applications
Developing a deep understanding of the temperature dependence of the rate constant equips students with the ability to:
Analyze and Interpret Graphs: Reading an Arrhenius plot to extract kinetic parameters like activation energy and the Arrhenius constant.
Perform Calculations: Using the Arrhenius equation to predict how a reaction's rate constant changes with temperature.
Conduct Experiments: Designing and executing experiments to measure reaction rates, applying the theory to practical scenarios.
Enhancing Experimental Design
Knowledge of how temperature influences reaction rates informs the design of experiments, allowing for more accurate control of reaction conditions. It also aids in troubleshooting experimental outcomes, where unexpected temperature fluctuations might cause deviations from predicted results.
Broadening the Perspective
While the focus here is on the temperature dependence of the rate constant, it's important to appreciate this in the context of broader chemical kinetics. The rate constant is just one piece of the puzzle in understanding reaction mechanisms, the effects of catalysts, and the role of intermediates in complex reactions.
Integration with Other Kinetic Concepts
The Arrhenius equation intersects with other areas of chemical kinetics, such as the study of catalysts that lower the activation energy, thus increasing the rate constant. It also ties into the study of reaction mechanisms, where the concept of the rate-determining step further refines our understanding of how reactions progress at the molecular level.
Conclusion
The exploration of the temperature dependence of the rate constant through the Arrhenius equation is a fundamental aspect of chemical kinetics. It not only deepens our understanding of how reactions occur but also provides a powerful tool for controlling and optimizing these reactions in various scientific and industrial applications. This knowledge is pivotal for students embarking on careers in chemistry, chemical engineering, and related fields, where the principles of reaction kinetics are applied to solve real-world problems.
FAQ
When calculating the rate constant (( k )) using the Arrhenius equation, the choice of temperature units is crucial due to its impact on the value of the universal gas constant (( R )). In the Arrhenius equation, ( k = Ae{-\frac{Ea}{RT}} ), temperature (( T )) must be in Kelvin (K) to ensure consistency with the units of ( R ) (8.314 J mol({-1}) K({-1})). Using temperatures in Celsius or Fahrenheit without conversion to Kelvin would lead to incorrect results because the value of ( R ) is specifically calibrated for use with Kelvin. Kelvin is an absolute temperature scale where 0 K represents absolute zero, the point at which particles have minimal thermal energy. This absolute scale ensures that the exponential term in the Arrhenius equation accurately represents the temperature-dependent energy distribution of molecules. Converting temperatures to Kelvin before applying the Arrhenius equation is essential to obtain accurate and meaningful rate constants, reflecting the true nature of the temperature's effect on reaction kinetics.
The Arrhenius equation provides a valuable model for understanding the temperature dependence of reaction rates under ideal conditions. However, its applicability to non-ideal conditions, such as reactions involving solid catalysts, heterogeneous mixtures, or non-ideal solutions, can be limited. In such cases, the assumptions underlying the Arrhenius equation, particularly the concept of a single, well-defined activation energy and a straightforward relationship between temperature and reaction rate, may not hold. For example, in heterogeneous catalysis, the surface properties of the catalyst, the diffusion of reactants to and from the surface, and the interactions at the interface can significantly influence the reaction rate, introducing complexities not accounted for by the Arrhenius equation. Similarly, in reactions involving complex mixtures or non-ideal solutions, interactions between different components can affect reaction kinetics in ways that the Arrhenius equation, with its focus on the temperature dependence of a single rate constant, might not fully capture. While the Arrhenius equation remains a foundational tool in chemical kinetics, its application to non-ideal conditions often requires modifications or supplementary models to accurately describe reaction behavior.
The Arrhenius constant (( A )), also known as the pre-exponential factor, is a crucial component of the Arrhenius equation that reflects the frequency of collisions between reactant molecules with the correct orientation for a reaction to occur. It encompasses factors beyond mere collision frequency, incorporating the probability that collisions have sufficient energy and the proper orientation to overcome the activation energy barrier. A high value of ( A ) suggests that a large number of collisions result in successful reactions, indicating either a high collision frequency or a favorable orientation of molecules during collisions. Conversely, a lower value of ( A ) might imply fewer effective collisions, possibly due to a more complex reaction mechanism or steric hindrance that reduces the probability of reactants approaching each other in an orientation conducive to reaction. Thus, the Arrhenius constant provides insight into the inherent reactivity and kinetic accessibility of a reaction pathway, reflecting both the physical and spatial aspects of molecular interactions that drive the reaction forward.
Catalysts influence the Arrhenius equation by lowering the activation energy (( Ea )) required for a reaction to proceed, thereby increasing the rate constant (( k )) and, consequently, the reaction rate. The presence of a catalyst provides an alternative reaction pathway with a lower energy barrier compared to the uncatalyzed reaction. This reduction in ( Ea ) leads to a higher proportion of reactant molecules having sufficient energy to overcome the activation energy barrier, even at lower temperatures. The effect of a catalyst on the Arrhenius constant (( A )) is more complex and can vary depending on the nature of the catalytic process. In some cases, ( A ) might increase due to the catalyst providing more favorable conditions for effective collisions, such as proper orientation or closer proximity of reactant molecules. The catalytic effect on the Arrhenius equation underscores the critical role of catalysts in enhancing reaction rates by modifying the energy landscape of the reaction without being consumed in the process.
In first-order reactions, the half-life, the time required for the concentration of a reactant to decrease to half its initial value, is directly related to the rate constant (( k )) and, by extension, to the Arrhenius equation. The half-life (( t{1/2} )) in first-order reactions is given by ( t{1/2} = \frac{\ln 2}{k} ), indicating that it is inversely proportional to the rate constant. Since the Arrhenius equation describes how ( k ) varies with temperature, it also indirectly determines how the half-life of a first-order reaction changes with temperature. As temperature increases, the rate constant increases according to the Arrhenius equation, leading to a decrease in the half-life. This relationship highlights the sensitivity of reaction kinetics to temperature changes and provides a practical way to understand the impact of temperature on the time scale of reactions. By manipulating temperature, chemists can control the rate at which reactants are converted to products, adjusting the half-life to suit specific industrial or laboratory needs.
When constructing the rate equation, the stoichiometry and the reactants involved in the rate-determining step are of primary importance. The orders of reaction in the rate equation correspond to the coefficients of the reactants in this step, not necessarily those in the overall balanced equation for the reaction. This means that even if a reactant appears in the overall reaction, it may not appear in the rate equation if it is not involved in the rate-determining step.
Understanding the rate-determining step allows chemists to predict and manipulate reaction rates more effectively. By altering conditions or concentrations of reactants involved in this crucial step, one can control the reaction speed, which is especially important in industrial processes where efficiency and optimization are key.
Practice Questions
Given a reaction with an activation energy of 60 kJ/mol, the rate constant doubles when the temperature is increased from 300 K to 310 K. Calculate the Arrhenius constant (A) for this reaction. Assume R = 8.314 J/mol·K.
An excellent A level Chemistry student's answer would demonstrate a clear understanding of the Arrhenius equation and its application to the given problem. The student would start by expressing the equation for the rate constant at two different temperatures, ( k1 = Ae{-\frac{Ea}{RT1}} ) and ( k2 = 2k1 = Ae{-\frac{Ea}{RT2}} ). By dividing the second equation by the first, the student would eliminate the Arrhenius constant and solve for ( A ) using the given values, showing detailed calculation steps. The final answer would correctly reflect the Arrhenius constant, calculated using the relationship ( \frac{k2}{k1} = e{-\frac{Ea}{R}(\frac{1}{T2} - \frac{1}{T1})} ), demonstrating a high level of proficiency in handling exponential equations and a deep understanding of chemical kinetics.
An experiment to determine the rate constant of a reaction at different temperatures yielded the following data: ln(k) = -5000/T + 10. Using this data, determine the activation energy (Ea) of the reaction and explain its significance.
A top-notch answer would begin by identifying that the given equation is a form of the linearised Arrhenius equation, ( ln(k) = -\frac{Ea}{R} \times \frac{1}{T} + ln(A) ). The student would correctly deduce that the slope of the line, -5000, is equal to ( -\frac{Ea}{R} ). By rearranging this relationship and solving for ( Ea ), the student would calculate the activation energy using the given slope and the value of ( R ). The answer would include a concise explanation of the significance of activation energy in determining the rate at which a chemical reaction proceeds, highlighting its role as the minimum energy barrier that reactants must overcome to form products. This response would demonstrate not only mathematical prowess but also a deep understanding of the conceptual underpinnings of chemical kinetics.
