Conventional Cell Representations
The accurate depiction of electrochemical cells is fundamental for grasping their operational principles and design intricacies.
Cell Diagrams
Cell diagrams provide a simplified yet informative representation of electrochemical cells, illustrating the components and their arrangement.
Anode and Cathode Identification: The anode, where oxidation occurs, is placed on the left side of the diagram, while the cathode, the site of reduction, is on the right. This convention aids in understanding the flow of electrons within the cell.
Electrode Representation: Electrodes are depicted by their elemental symbols (e.g., Zn for zinc, Cu for copper) when solid, and their ionic forms (e.g., Zn2+, Cu2+) when in solution, providing clarity on the participating species in the cell's redox reactions.
Salt Bridge: Illustrated by a double vertical line (||), the salt bridge is crucial for maintaining electrical neutrality by facilitating the flow of ions between the half-cells, thus completing the cell circuit.
Phase Boundaries: Denoted by single vertical lines (|), phase boundaries separate different phases within the cell, such as a solid electrode from an aqueous electrolyte solution, helping to visualise the cell's structure.
Example of Cell Representation
A classic example is the Daniell cell, represented as Zn(s) | Zn2+(aq) || Cu2+(aq) | Cu(s). This notation succinctly captures the cell's components, with zinc undergoing oxidation and copper undergoing reduction.
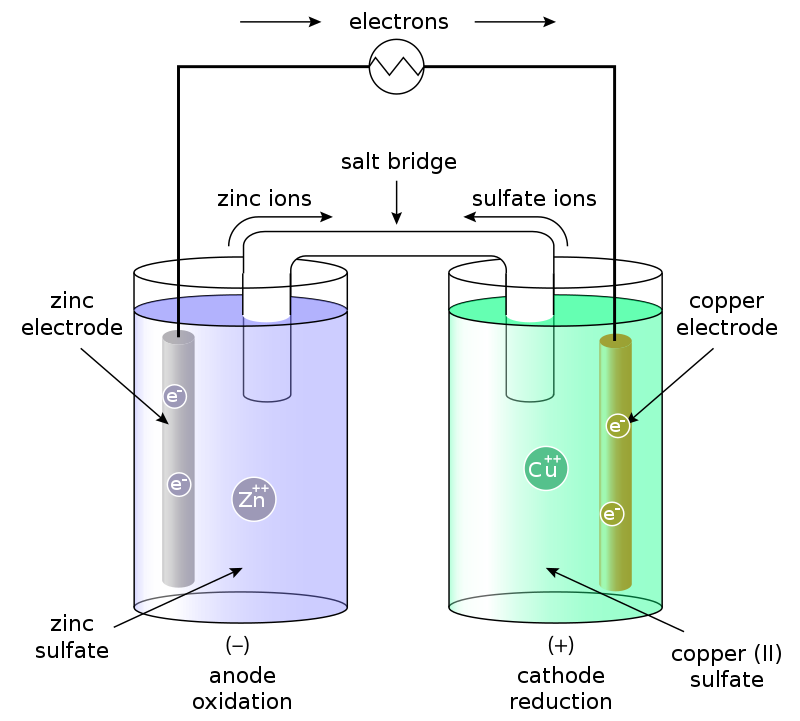
Image courtesy of Rehua
EMF Calculations
The EMF of a cell is a critical parameter, indicative of the cell's capability to drive an electric current through an external circuit.
Standard Electrode Potentials (E°)
Conceptual Foundation: The standard electrode potential is defined as the potential difference between a half-cell and the standard hydrogen electrode (SHE), under standard conditions (298 K, 1 atm, 1 M concentration of ions).
Role of SHE: With a defined potential of 0.00 V, the SHE serves as a universal reference, enabling the measurement and comparison of electrode potentials for various half-cells.
Utility: E° values are indispensable for predicting redox reaction directions and for calculating the EMF of electrochemical cells, laying the groundwork for understanding cell dynamics.
Image courtesy of Reuel Sa
Skills: Determining
Nernst Equation
The Nernst equation extends the application of standard electrode potentials to conditions that deviate from the standard, incorporating the influence of concentration on the cell's EMF:
[ E = E° - \frac{RT}{nF} \ln Q ]
Here, E represents the cell EMF, E° the standard EMF, R the universal gas constant, T the temperature in Kelvin, n the number of electrons involved in the reaction, F the Faraday constant, and Q the reaction quotient.
Calculating Cell EMF
Under Standard Conditions: When conditions are standard, the reaction quotient Q is 1, simplifying the Nernst equation to E = E°, making the calculation straightforward.
Determining Cell Potential: The overall EMF of the cell, E, is determined by subtracting the anode potential from the cathode potential: Ecell = E°cathode - E°anode. This difference provides the driving force for the electrical current in the cell.
Practical Applications
The theoretical concepts of EMF calculations find real-world application in the development and optimisation of various electrochemical devices.
Battery Design
Electrode Material Selection: The efficiency and capacity of batteries are significantly influenced by the choice of materials for the anode and cathode, guided by their standard electrode potentials to achieve a desirable EMF.
Optimisation Through Conditions: Fine-tuning the concentration of electrolytes and operating temperature can enhance a battery's performance, with the Nernst equation providing the theoretical basis for such adjustments.
Fuel Cells
Efficiency Enhancement: The Nernst equation plays a pivotal role in analysing and enhancing the efficiency of fuel cells under varying operational conditions, contributing to the advancement of clean energy technologies.
Image courtesy of rawpixel.com on freepik
Analytical Representation of Cells
Beyond mere diagrammatic representation, the analytical approach to electrochemical cells involves a deep understanding of the implications of cell design and conditions on their functionality.
Interpreting Cell Diagrams
Direction of Redox Reactions: The standard electrode potentials enable the prediction of the direction in which the redox reactions will proceed, with the higher potential half-cell typically undergoing reduction.
Identifying Performance Limitations: Factors such as electrolyte concentration and temperature can impact cell performance, with their effects analytically assessable through the Nernst equation.
EMF and Cell Efficiency
EMF Optimisation: For optimal efficiency, the selection of electrode materials and the conditions under which the cell operates must be strategically chosen to maximise the EMF.
Thermodynamics Link: The relationship between the Gibbs free energy change (ΔG) and the EMF of the cell, expressed as ΔG = -nFE, underscores the thermodynamic efficiency of the cell and its practical energy conversion capabilities.
In synthesising the conventional representations with the mathematical framework for EMF calculations, this section offers a comprehensive exploration of electrochemical cells. This foundation is not only academically enriching but also practically applicable in the realms of energy storage and conversion, embodying the principles that underpin advancements in battery and fuel cell technologies. Through a detailed understanding of these concepts, students are equipped to navigate the complexities of electrochemistry, fostering innovations that drive forward the fields of sustainable energy and materials science.
FAQ
The Nernst equation demonstrates that the EMF of an electrochemical cell is not a fixed value but can vary with changes in the concentration of the reactants and products. As concentration plays a role in the reaction quotient ( Q ) in the Nernst equation ( E = E° - \frac{RT}{nF} \ln Q ), variations in ion concentrations directly affect the cell's EMF. For a cell reaction, as the concentration of the reactants decreases (or the products increases), the value of ( Q ) increases, leading to a larger negative term in the Nernst equation, thus reducing the cell's EMF. Conversely, increasing the concentration of reactants (or decreasing the concentration of products) decreases ( Q ), resulting in a smaller negative term and a higher EMF. This relationship underscores the dynamic nature of electrochemical cells, where the EMF is sensitive to the chemical environment, allowing for the fine-tuning of cell performance through concentration adjustments.
A salt bridge is crucial in an electrochemical cell as it serves to maintain electrical neutrality within the half-cells by allowing the transfer of ions. During the redox reactions at the electrodes, electrons are transferred through the external circuit, leading to a build-up of charge that would eventually stop the reaction due to electrostatic repulsion. The salt bridge contains a salt solution that releases ions; cations move towards the cathode compartment, and anions move towards the anode compartment. This ion movement balances the charges that accumulate as a result of electron flow, ensuring the continuous operation of the cell. Furthermore, the salt bridge prevents the direct mixing of the different solutions in the half-cells, which could lead to precipitation of reaction products and interfere with the cell's function. Therefore, the salt bridge is essential for the sustained and efficient operation of electrochemical cells.
Temperature has a significant impact on the EMF of an electrochemical cell, as indicated by the term ( \frac{RT}{nF} ) in the Nernst equation. As temperature increases, the value of ( RT ) increases, leading to a higher value of the entire term ( \frac{RT}{nF} \ln Q ), assuming that ( Q ), ( n ), and ( F ) remain constant. This results in a greater reduction of the cell's EMF from its standard value. The increase in temperature typically enhances the kinetic energy of the reacting species, potentially accelerating the reaction rate and influencing the equilibrium position of the cell reactions. These changes can alter the concentration of reactants and products, further affecting the EMF through the reaction quotient ( Q ). Therefore, temperature not only directly affects the EMF through the Nernst equation but also indirectly by changing the reaction dynamics within the cell.
The standard hydrogen electrode (SHE) plays a pivotal role in electrochemistry as the universal reference electrode against which the standard electrode potentials of all other electrodes are measured. The SHE consists of a platinum electrode in contact with 1 M H⁺ ions and bathed in hydrogen gas at 1 atm pressure. It is assigned a potential of 0.00 V under standard conditions (298 K, 1 atm, and a 1 M concentration of ions). This arbitrary assignment provides a baseline for comparing electrode potentials, ensuring consistency and comparability in electrochemical measurements. The SHE is essential for constructing electrochemical series, which ranks elements according to their electrode potentials, facilitating the prediction of redox reaction directions and the spontaneity of chemical processes. Its widespread acceptance and use in electrochemistry underscore its importance in understanding and applying electrochemical principles.
Determining the anode and cathode in an electrochemical cell involves identifying where oxidation and reduction reactions occur, respectively. The anode is the electrode at which oxidation, the loss of electrons, takes place, while the cathode is where reduction, the gain of electrons, occurs. This determination can be made by analyzing the standard electrode potentials of the involved half-reactions; the half-cell with the lower (more negative) standard electrode potential tends to be the anode, as it has a greater tendency to lose electrons. Conversely, the half-cell with the higher (more positive) standard electrode potential tends to be the cathode, as it has a greater tendency to gain electrons. In a galvanic (voltaic) cell, the anode is negative because it is the source of electrons that flow through the external circuit to the cathode, which is positive. In an electrolytic cell, the anode is positive because it is connected to the positive pole of the power supply, driving the oxidation reaction, whereas the cathode is negative, facilitating reduction.
Practice Questions
Describe the cell representation for a galvanic cell consisting of a magnesium electrode in 1 M Mg²⁺ solution and a silver electrode in 1 M Ag⁺ solution. Include the anode, cathode, and the salt bridge in your description. Explain the direction of electron flow in this cell.
The cell is represented as Mg(s) | Mg²⁺(1M) || Ag⁺(1M) | Ag(s), where magnesium acts as the anode and silver as the cathode. The magnesium electrode undergoes oxidation, losing electrons to form Mg²⁺ ions, while the silver electrode undergoes reduction, gaining electrons to deposit silver metal. Electrons flow from the magnesium electrode to the silver electrode through the external circuit, driven by the difference in standard electrode potentials. The salt bridge maintains electrical neutrality by allowing the movement of ions, completing the circuit and enabling the flow of electrons.
Given the standard electrode potentials E°(Ag⁺/Ag) = +0.80 V and E°(Mg²⁺/Mg) = -2.37 V, calculate the standard EMF of the cell described in Question 1. Explain the significance of the sign and magnitude of the EMF value.
The standard EMF (E_cell) of the cell can be calculated using the formula Ecell = E°cathode - E°anode. Here, E°cathode (Ag⁺/Ag) is +0.80 V and E°anode (Mg²⁺/Mg) is -2.37 V. Thus, Ecell = +0.80 V - (-2.37 V) = +3.17 V. The positive sign of the EMF indicates that the cell reaction is spontaneous, and the magnitude of 3.17 V signifies a strong driving force for the electron flow from magnesium to silver. This high EMF value reflects the cell's ability to do work and its potential application in generating electrical energy.
