AQA Specification focus:
'- Definitions and distinctions between lattice dissociation enthalpy and lattice formation enthalpy.
- Understanding the relevance and application of lattice enthalpy in thermodynamics.'
Introduction to Lattice Enthalpy
Lattice enthalpy embodies the energy dynamics involved in the making and breaking of ionic lattices. It's a concept that bridges the microscopic ionic interactions with macroscopic physical properties, offering insights into the energetic landscape of ionic compounds.
Lattice Formation Enthalpy
Definition: The lattice formation enthalpy (( \Delta H{\text{formation}} )) is defined as the energy change accompanying the formation of one mole of an ionic compound from its gaseous ions under standard conditions.
Exothermic Nature: The process is invariably exothermic, signifying that energy is released as the lattice is formed. This release of energy is a testament to the stability imparted to the compound through lattice formation.
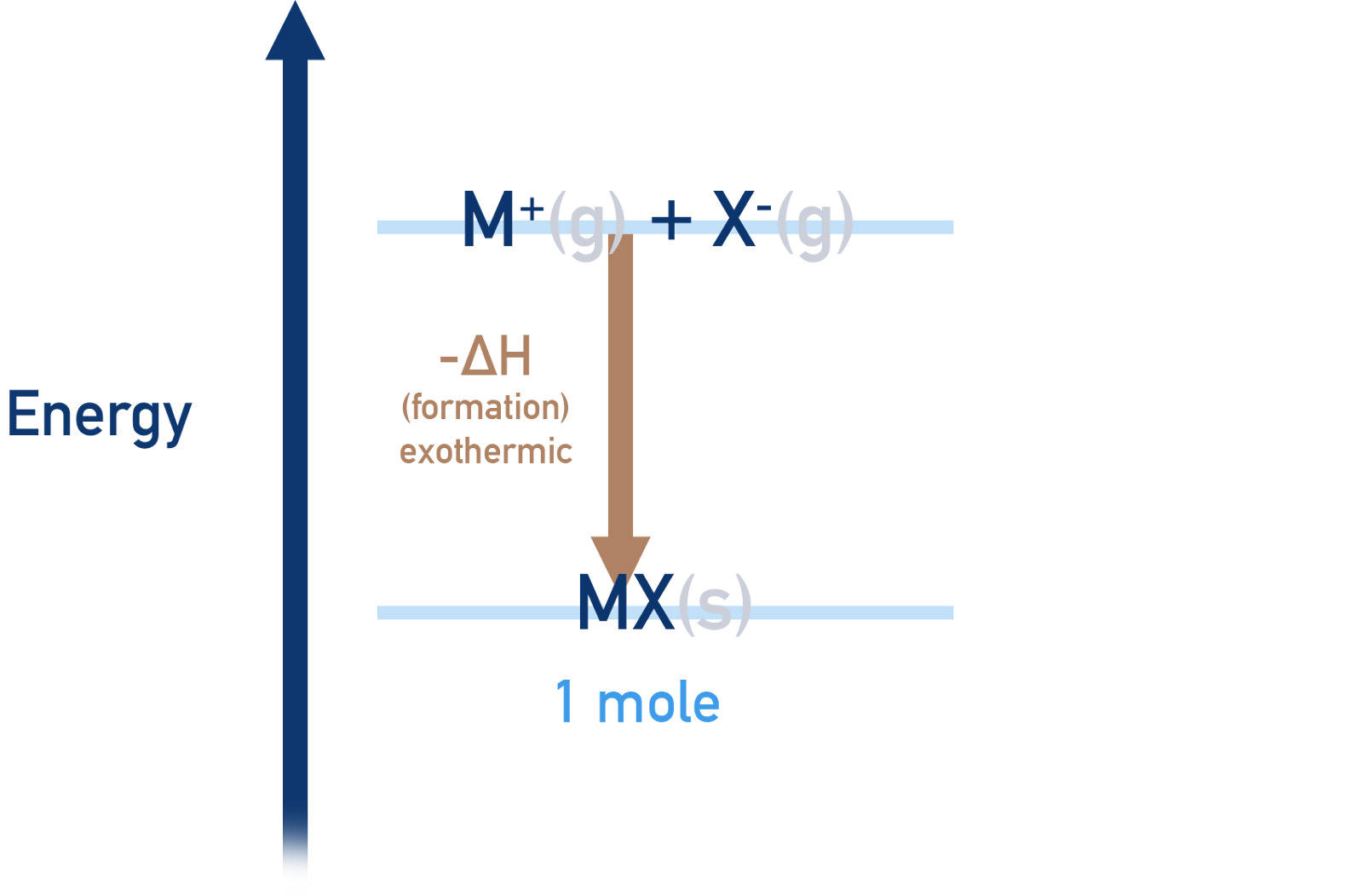
Image courtesy of ChemistryStudent
Lattice Dissociation Enthalpy
Definition: Conversely, the lattice dissociation enthalpy (( \Delta H{\text{dissociation}} )) is the energy required to separate one mole of an ionic lattice into its constituent gaseous ions under standard conditions.
Endothermic Process: This process is endothermic, reflecting the necessity of energy input to disrupt the electrostatic forces anchoring the ions within the lattice.
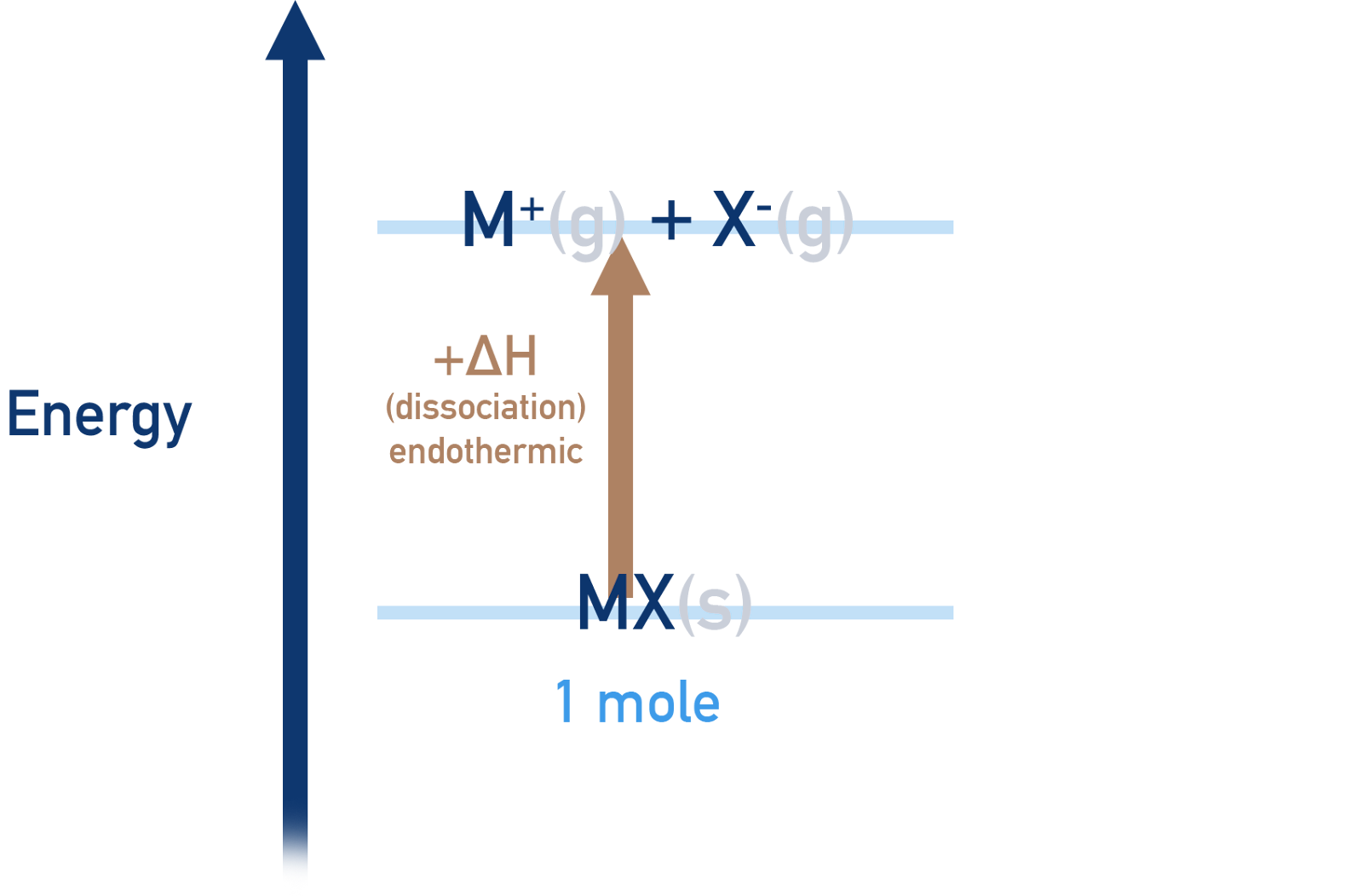
Image courtesy of ChemistryStudent
Distinctions Between Formation and Dissociation Enthalpies
The conceptual distinction between lattice formation and dissociation enthalpies is crucial for a nuanced understanding of lattice enthalpy as a whole.
Process Directionality: Formation concerns the energy-releasing assembly of the lattice, whereas dissociation involves the energy-consuming disassembly.
Thermodynamic Nature: Formation processes are characterised by their exothermicity, in contrast to the endothermic nature of dissociation processes.
Ionic Compound Stability: The magnitude of these enthalpies is indicative of the ionic bonds' strength and, by extension, the compound's overall stability.
Thermodynamic Relevance and Applications
Lattice enthalpy transcends theoretical chemistry, finding practical applications in predicting ionic compounds' stability and physical attributes.
Predicting Physical Properties
Melting and Boiling Points: High lattice enthalpies correlate with elevated melting and boiling points, attributable to the robust electrostatic interactions between ions.
Solubility: Lattice enthalpy influences an ionic compound's solubility, with lower lattice enthalpies generally enhancing solubility in solvents like water.
Stability and Formation of Ionic Compounds
Contribution to Stability: The exothermic lattice formation enthalpy significantly bolsters an ionic compound's stability, making high lattice enthalpies synonymous with greater stability.
Role in Thermodynamic Cycles: Lattice enthalpy is integral to thermodynamic cycles, such as Born–Haber cycles, facilitating the calculation of ionic compounds' formation enthalpies.

Born–Haber cycle
Image courtesy of Jkwchui
Thermodynamic Calculations and Models
Hess's Law Application: Indirect calculation of lattice enthalpies utilises Hess's Law, asserting the constancy of total enthalpy change across a reaction, irrespective of the path taken.
Born–Haber Cycle Utilisation: This practical application of Hess's Law employs lattice enthalpy alongside other thermodynamic data to elucidate the formation enthalpies of ionic compounds.
In-Depth Exploration of Lattice Enthalpy
A deeper dive into the determinants of lattice enthalpy and the models used for its estimation reveals the complexity and significance of this concept.
Influential Factors
Ionic Radii: Smaller ions typically lead to compounds with more significant lattice enthalpies due to the intensified electrostatic attractions arising from their closer proximity.
Charge Magnitude: Higher ionic charges result in increased lattice enthalpies because of the augmented electrostatic forces between such ions.

Image courtesy of saylordotorg.github.io
Estimation Models
Born–Landé Equation: This equation provides a method to estimate the lattice enthalpy of ionic compounds by considering the ions' charges, their separation distances, and the lattice's ionic arrangement.
Kapustinskii Equation: Serving as a simplified method, this equation estimates lattice enthalpies based on ionic radii and charges, particularly useful when detailed ionic arrangements are unknown.
Practical Implications of Lattice Enthalpy
The significance of lattice enthalpy extends to various fields, including materials science, pharmaceuticals, and energy storage, underlining its broad applicability.
Materials Science Applications: Knowledge of lattice enthalpies aids in designing new materials with specific melting points, solubilities, and other tailored physical properties.
Pharmaceutical Relevance: In pharmaceuticals, the solubility of drugs—a critical factor for their effectiveness—can be influenced by the lattice enthalpy of their ionic forms.
Energy Storage Innovations: In energy storage solutions like batteries, lattice enthalpy contributes to determining the stability and reactivity of electrolytic ionic compounds.
Conclusion
Lattice enthalpy serves as a fundamental concept within thermodynamics, bridging the gap between ionic interactions at the microscopic level and the macroscopic physical properties of compounds. Its comprehensive understanding is indispensable for students, offering a window into the energetic considerations of ionic bonding and its ramifications across various scientific and industrial domains. Through a detailed exploration of lattice formation and dissociation enthalpies, their distinctions, and their applications, students gain valuable insights into the stability, formation, and inherent properties of ionic compounds, underscoring the importance of lattice enthalpy in the broader context of chemistry and materials science.
FAQ
The lattice formation enthalpy is always exothermic due to the nature of ionic bond formation. When gaseous ions come together to form a lattice structure, the electrostatic forces of attraction between the oppositely charged ions release a significant amount of energy. This release of energy is a result of the system moving towards a more stable, lower energy state, which characterises exothermic reactions. In contrast, lattice dissociation enthalpy is endothermic because breaking the ionic bonds within the lattice structure requires an input of energy. Overcoming the electrostatic forces of attraction between the ions demands energy to move the ions apart, which increases the system's energy, typical of endothermic processes. The distinction between these two types of enthalpies underscores the fundamental principles of chemical thermodynamics, where bond formation releases energy and bond breaking consumes energy.
The charge of ions has a profound impact on the magnitude of lattice enthalpy due to the electrostatic force law, which states that the force between two charged particles is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. In ionic compounds, higher ionic charges result in stronger electrostatic attractions between the ions, leading to higher lattice enthalpies. For instance, an ionic compound formed from ions with charges of +2 and -2 will have a significantly higher lattice enthalpy than a compound formed from ions with charges of +1 and -1, assuming the ionic sizes are comparable. This is because the electrostatic force, and thus the energy released upon formation of the lattice, increases with the increase in the magnitude of the charge on the ions. Therefore, the charge on the ions is a critical factor in determining the stability and energy characteristics of ionic compounds.
Lattice enthalpy cannot be measured directly because it involves the hypothetical process of forming an ionic compound from its gaseous ions or dissociating an ionic solid into gaseous ions, which is not feasible to perform under standard laboratory conditions. Instead, lattice enthalpy is determined indirectly using experimental data and Hess's Law, which states that the total enthalpy change for a chemical reaction is the same, regardless of the route by which the chemical reaction takes place. One common method involves the use of a Born–Haber cycle, a thermochemical cycle that relates various steps involved in the formation of an ionic compound from its constituent elements, including ionisation energy, electron affinity, enthalpy of formation, and sublimation energy. By combining these measurable thermodynamic quantities, the lattice enthalpy can be calculated indirectly, providing valuable insights into the energetics of ionic compounds.
Smaller ions lead to compounds with higher lattice enthalpies due to the shorter distance between the nuclei of the ions, which enhances the electrostatic force of attraction between them. According to Coulomb's law, the force of attraction (or repulsion) between two charged particles is inversely proportional to the square of the distance between their centres. In the context of ionic compounds, as the size of the ions decreases, the distance between the centres of the positive and negative ions reduces, resulting in a stronger electrostatic attraction. This stronger attraction means that more energy is released when these ions come together to form a lattice, leading to a higher lattice formation enthalpy. Conversely, larger ions, with their larger internuclear distances, exhibit weaker attractions and consequently lower lattice enthalpies. Therefore, the size of the ions is a critical factor in determining the energy characteristics and stability of ionic compounds.
Lattice enthalpy plays a crucial role in real-world applications, particularly in material design and pharmaceuticals, by influencing the physical properties and stability of compounds. In materials science, understanding the lattice enthalpy of ionic compounds allows chemists and engineers to predict and tailor properties such as melting point, hardness, and electrical conductivity, which are essential for designing materials for specific applications. For example, compounds with high lattice enthalpies are used to create heat-resistant materials and ceramics.
In the pharmaceutical industry, the solubility of drugs is a key factor in their effectiveness, as it affects absorption and bioavailability. Lattice enthalpy influences the solubility of ionic compounds, including many drugs. Lower lattice enthalpies often correspond to higher solubility in water, making the active ingredients more readily absorbed by the body. By manipulating the lattice enthalpy through the design of drug molecules or the formation of salts, pharmaceutical chemists can enhance the solubility and, consequently, the efficacy of medications. Thus, the concept of lattice enthalpy is integral to the development and optimisation of materials and drugs, showcasing the practical applications of this fundamental thermodynamic concept.
Practice Questions
Define lattice formation enthalpy and lattice dissociation enthalpy. Explain how these two enthalpies are related to the stability of an ionic compound.
Lattice formation enthalpy is the energy released when one mole of an ionic compound forms from its gaseous ions under standard conditions, and it is always exothermic. Lattice dissociation enthalpy is the energy required to separate one mole of an ionic compound into its gaseous ions, an endothermic process. The magnitude of these enthalpies indicates the strength of the electrostatic forces between ions in the lattice. A higher lattice formation enthalpy suggests a more stable ionic compound because more energy is released upon formation, signifying stronger ionic bonds and greater compound stability.
Describe how lattice enthalpy can influence the physical properties of an ionic compound, specifically melting point and solubility.
Lattice enthalpy significantly impacts an ionic compound's melting point and solubility. A high lattice enthalpy indicates strong electrostatic forces between ions, leading to higher melting points as more energy is required to overcome these forces for the compound to change state from solid to liquid. Regarding solubility, compounds with lower lattice enthalpies are generally more soluble in water because less energy is needed to disrupt the ionic lattice for the ions to be hydrated by water molecules. Thus, lattice enthalpy is a key factor in determining the physical behaviour of ionic compounds in various conditions.

